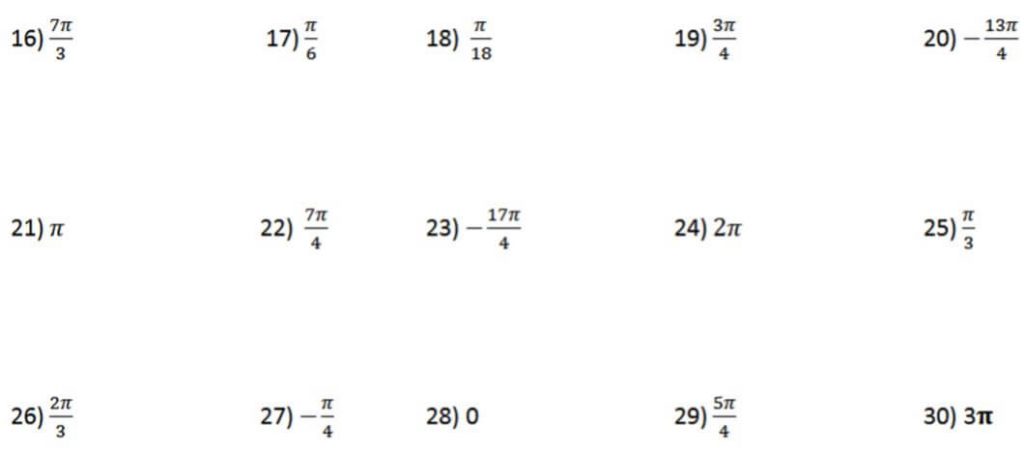What are Trigonometric functions

Why do we need to Study Trigonometric Functions ?
Without knowing Trigonometric functions, we wouldn’t be able to solve Probems in, Science, Engineering, Technology, Artificial Intelligence, Architecture and Medicine. Now it is important to know that all of the Developments in the World that we live in owes its dues to the above Areas. For what could we do without these Modern Marvels that had totally eased many of the challenges.
Now it is also important to know that the gadgets made using modern technology will have issues and one need to troubleshoot them. So in order to be able to troubleshoot, you need to understand how they work, and to understand how they work, you need Trigonometric functions. Of course there are other areas too that work together, but as for the Math part is concerned, learning and knowing Trigonometric functions is of critical importance.
Now the first step in understanding Trigonometric functions is to understand, Angles, how they are measured, their types and solving related problems.


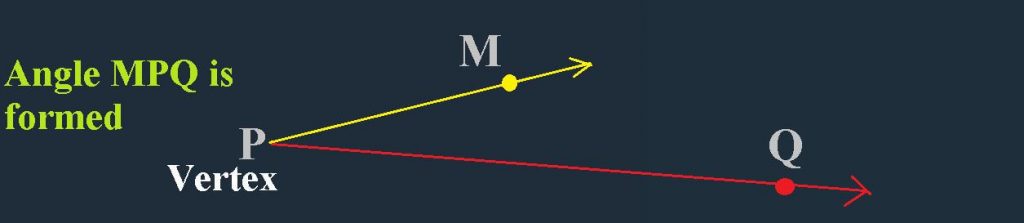
Now let us understand what an Angle is ?
An angle is formed at the union of two Rays that have a common endpoint. The endpoint is called the Vertex of the angle, and the two rays are the sides of the angle.
Greek letters are used as Variables to represent the Angle measures. We give below the popular Greek letters used .

What is the measure of an Angle
Angles are the heart and muscle of Trigonometry. In fact, there can be no Buildings without Angles, and more so, no Building can be constructed Perfectly symmetric without knowing how to Measure them
Angle measure = Amount of rotation from the Initial side to the Terminal side
There are two units used to measure an Angle and they are Degrees and Radians

Important: When you measure an Angle in degrees, make sure to place the Unit (word), "degrees" after the number, or use the degree symbol. Answers without the respective unit is considered Incorrect.
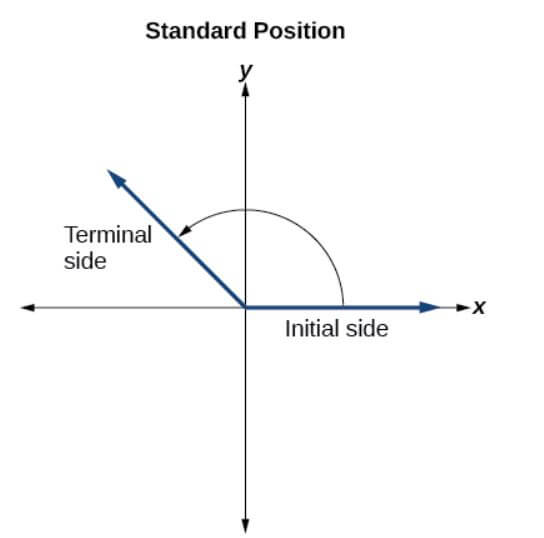
When is an Angle in standard position?
An Angle is in standard position, if its vertex is located at the Origin, and its Initial side extends along the positive side of the X-axis
When is an Angle a positive Angle ?
If the Angle is measured from the Initial side to the Terminal side, along the Anticlockwise direction (Counter Clockwise direction), then the Angle is said to be a positive Angle
When is an Angle a negative Angle ?
If the Angle is measured from the Initial side to the Terminal side, along the Clockwise direction, then the angle is said to be a negative Angle
What are Quadrantal Angles ?
Quadrantal angles are angels in the standard position whose terminal side lies on an axis, including 0°, 90°, 180°, 270°, or 360°. Given below are examples of Quadrantal angles.
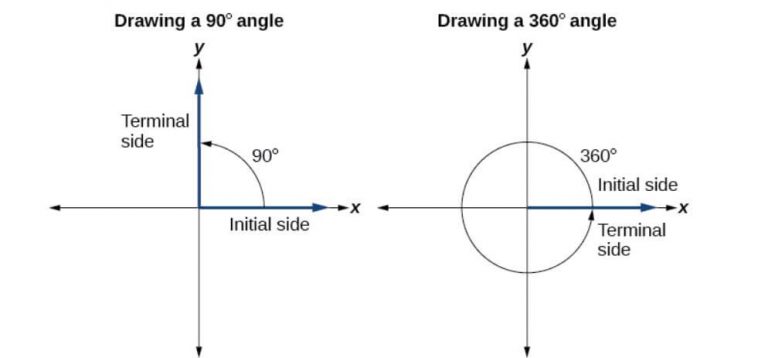
Observe that the Terminal side lies on the Axis
Try it: Express Quadrant angles as a fraction of 360 degree and draw the representation.
Example : Draw the angle of 30 degrees in Standard position
Solution

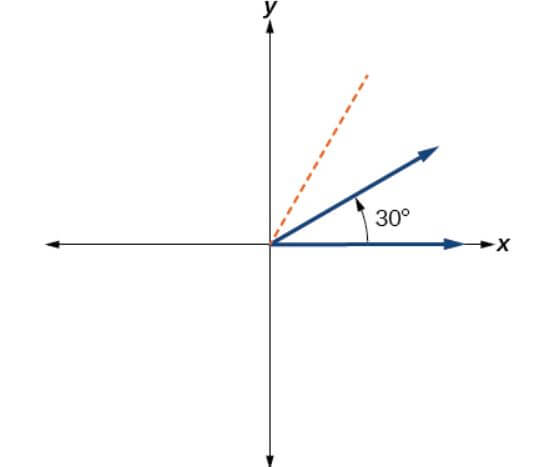
Try this: Sketch -135 degrees in Standard form
Sketch 240 degrees in Standard form
Now having studied and understood what an Angle is and how they are measured, let us now study the different types of Angles that we would encounter during this Course
Types of Angles
There are 5 Types of Angles, they are, Acute Angle, Right Angle, Obtuse Angle, Straight Angle and Reflex Angle.
Acute Angle : Angles that are between 0 degrees and 90 degrees.
Right Angle: Angles which are strictly 90 degrees.
Obtuse Angle: Angles which are between 90 degrees and 180 degrees. The Obtuse is from the Latin word Obtusus, meaning “Dull” or “blunt”, something which isn’t sharp.
Straight Angle: Angles which are 180 degrees
Reflex Angles: Angles which are between 180 degrees and 360 degrees.
Degrees, Minutes and Seconds (DMS)
Here we will learn how to convert a given Coordinate system in DMS into complete Degrees.
Convert 36o23’40” to decimal degrees
36o = 36o
We don’t need to do anything with the Degree part.
23′ = 23/60 = 0.38333o
40″ = 40/3600 = 0.01111o
Now Adding all we get = 36.3944o
What is a Radian measure ?
It is nothing but measuring the Angles using the Radius of a Circle.
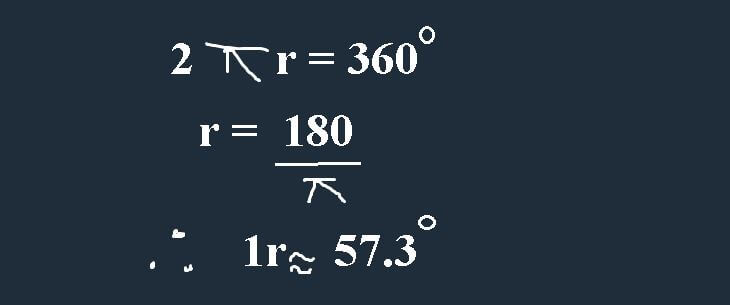
You can also find the value of 1 degree in terms of radians

Example 1

Example 2

Example 3
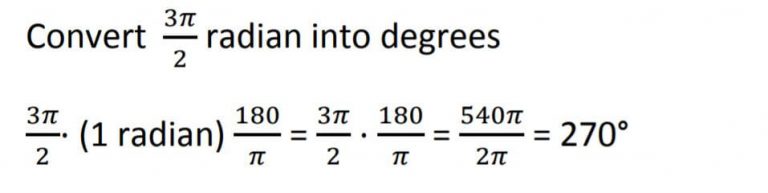
Example 4
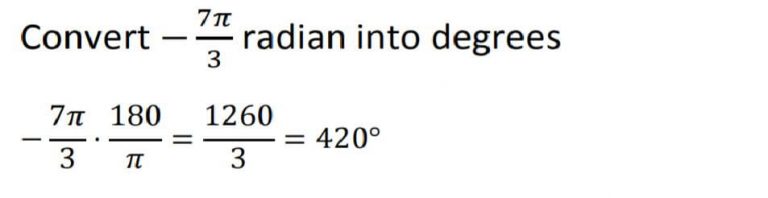
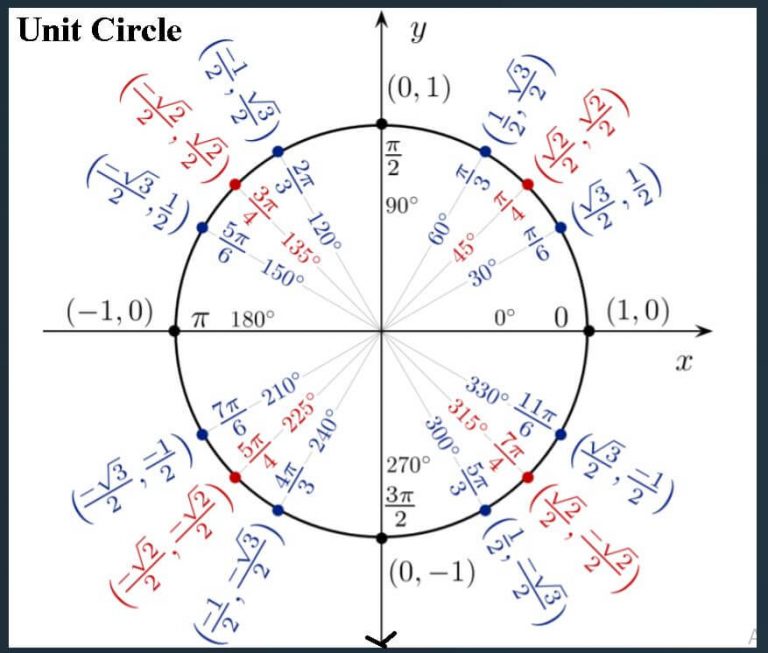
Now Let us Understand the Unit Circle
Understanding the Unit Circle is very Important. For one part of Trigonometry completely deals with Using concepts of the Unit Circle to solve Problems. Hence it is important that every Student puts in time and effort in memorizing this golden code.
Task 1: Convert the following Degree Measures to Radian Measures